The realm of quantum computing is rapidly evolving, with researchers striving to unlock the untapped potential of quantum simulators. At the forefront of this endeavor are advancements made by a collaborative team from Freie Universität Berlin, the University of Maryland, NIST, Google AI, and an institution in Abu Dhabi. Their work centers on estimating the Hamiltonian parameters that describe the dynamics of bosonic excitations within a superconducting quantum simulator. The implications of this research transcend the capabilities of classical computers, setting the stage for future quantum simulations with unparalleled precision.
Despite the profound interest and excitement surrounding superconducting quantum systems, the technical challenges associated with accurately determining Hamiltonian parameters have persisted. The complexities in measuring Hamiltonian dynamics, particularly due to the nature of quantum systems where traditional understanding often falls short, necessitate innovative approaches. The research team’s journey began with a conversation that illuminated these difficulties and ultimately led to new methodologies aimed at overcoming them.
The Inception of a Collaborative Solution
The initial thrust for this research occurred when Jens Eisert, the lead author, faced a perplexing problem posed by colleagues in Brazil. During a conference, he learned that the Google AI team was struggling with calibration issues related to their Sycamore superconducting chip due to inadequacies in Hamiltonian learning methods. Despite Eisert’s initial confidence in addressing the problem, it became evident that the challenge was far more intricate. The frequencies of the Hamiltonian operator were not being accurately captured, hindering the identification of the unknown Hamiltonian structures.
In a bid to approach this conundrum, Eisert enlisted the help of talented Ph.D. students, Ingo Roth and Dominik Hangleiter. Their combined efforts led to the exploration of superresolution techniques, a method aimed at enhancing the precision of eigenvalue estimations. This collaboration laid the foundation for years of dedicated research, during which the team refined their understanding and developed robust techniques necessary for real-world application.
Innovative Techniques: Superresolution and Manifold Optimization
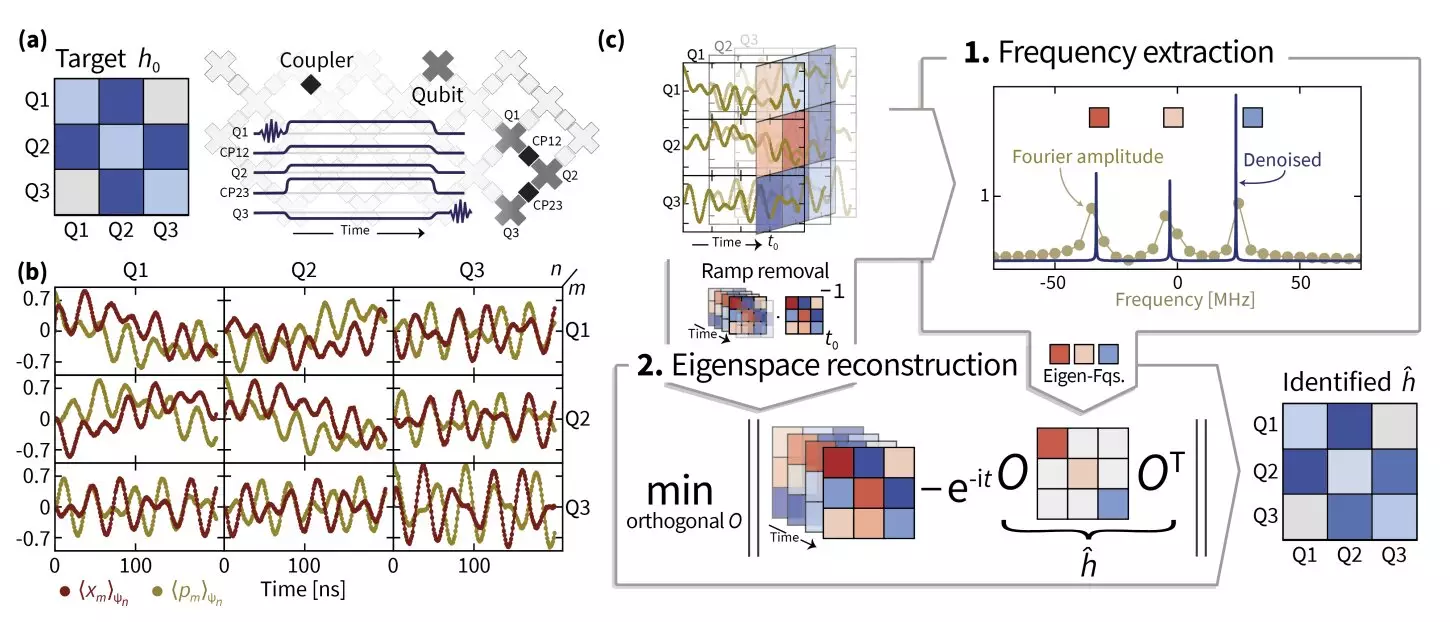
The team employed a multifaceted approach to unravel the intricacies of Hamiltonian dynamics. A significant breakthrough came from the utilization of superresolution, allowing for better resolution in eigenvalue estimation. This method was complemented by manifold optimization—a strategy particularly useful for addressing complex problems where variables do not reside in straightforward Euclidean spaces. These advanced optimization techniques enabled the researchers to recover the eigenspaces of the Hamiltonian operator with greater accuracy.
Eisert emphasized the significance of acknowledging imperfections in the processes necessary for Hamiltonian measurements. Understanding the real-world challenges of switching operations and their non-instantaneous nature proved crucial in creating a coherent framework for recovering Hamiltonian data. As the researchers progressed, they introduced a new method named TensorEsprit—a novel superresolution technique. By integrating TensorEsprit with manifold optimization, they ultimately identified Hamiltonian parameters for a system of up to 14 superconducting qubits distributed across two Sycamore processors.
This groundbreaking research highlights the essential concept of learning the Hamiltonian from empirical data. The findings point to the critical realization that a precise characterization of Hamiltonians not only provides insights into the quantum systems being studied, but also facilitates advancements in quantum technologies. However, the complexities involved in Hamiltonian learning have historically limited the volume of practical data reported in the literature, underscoring the importance of the breakthroughs achieved by Eisert and his colleagues.
As they delve deeper into their research, the team anticipates that the proposed techniques will prove to be scalable for larger quantum processors. They aim to apply their methods to interacting quantum systems and explore the potential of integrating ideas from tensor networks into studies of cold atomic systems—an area pioneered by physicist Immanuel Bloch.
Beyond their contributions to theoretical understanding, Eisert’s team’s future research endeavors hold considerable promise for practical applications in quantum technology. The capacity to characterize analog quantum simulators effectively can pave the way for high-precision quantum simulations. Such advancements could revolutionize our understanding of complex quantum systems and materials, enabling researchers to recreate intricate models under controlled laboratory conditions.
Eisert stressed the necessity of accurate Hamiltonian characterization, asserting that a precise understanding of Hamiltonians is crucial for predictive power in quantum mechanics. As this research progresses, it offers a fresh perspective on a long-standing question within the field: how can we learn Hamiltonians from empirical data? The resolutions on the horizon could significantly contribute to our grasp of quantum mechanics and herald the next generation of quantum technologies.
In essence, the journey of these researchers serves as a testament to the complexities and triumphs inherent in the quest for a deeper understanding of quantum systems. With their innovative techniques paving the way, the field stands on the brink of transformative breakthroughs that could reshape the landscape of quantum computing.

Leave a Reply