Artists who bring characters to life in animated movies and video games always strive for greater control over their animations. Recently, MIT researchers have introduced a groundbreaking technique that could grant artists this precise control. By generating mathematical functions called barycentric coordinates, artists can now define how 2D and 3D shapes can bend, stretch, and move through space. This technique not only empowers artists but also holds promise for various applications such as medical imaging, architecture, virtual reality, and computer vision. Let’s delve deeper into this innovative approach and explore its potential impact on the world of animation and beyond.
Traditionally, animating 2D or 3D characters involved surrounding their complex shapes with simpler points connected by line segments or triangles known as a cage. Animators would then manipulate these points to deform the character within the cage. However, the challenge lies in determining how the character moves when the cage is modified, and this motion depends on the design of a specific barycentric coordinate function. Previous approaches offered limited flexibility and required artists to start from scratch whenever they wanted to achieve a slightly different look. The researchers sought a more versatile approach that allows artists to have a say in designing or selecting smoothness energies for any shape. By doing so, artists can preview and choose the deformation that best suits their artistic vision.
To accomplish this goal, the MIT researchers utilized a special type of neural network to model the barycentric coordinate functions. Neural networks, inspired by the human brain, process inputs through interconnected nodes across multiple layers. In this context, the researchers employed neural networks not for artificial intelligence but for their mathematical prowess. The network architecture was designed to output barycentric coordinate functions that satisfy constraints exactly, ensuring the validity of the solutions. By building the constraints directly into the network, artists can focus on designing interesting barycentric coordinates without getting entangled in complicated mathematical aspects.
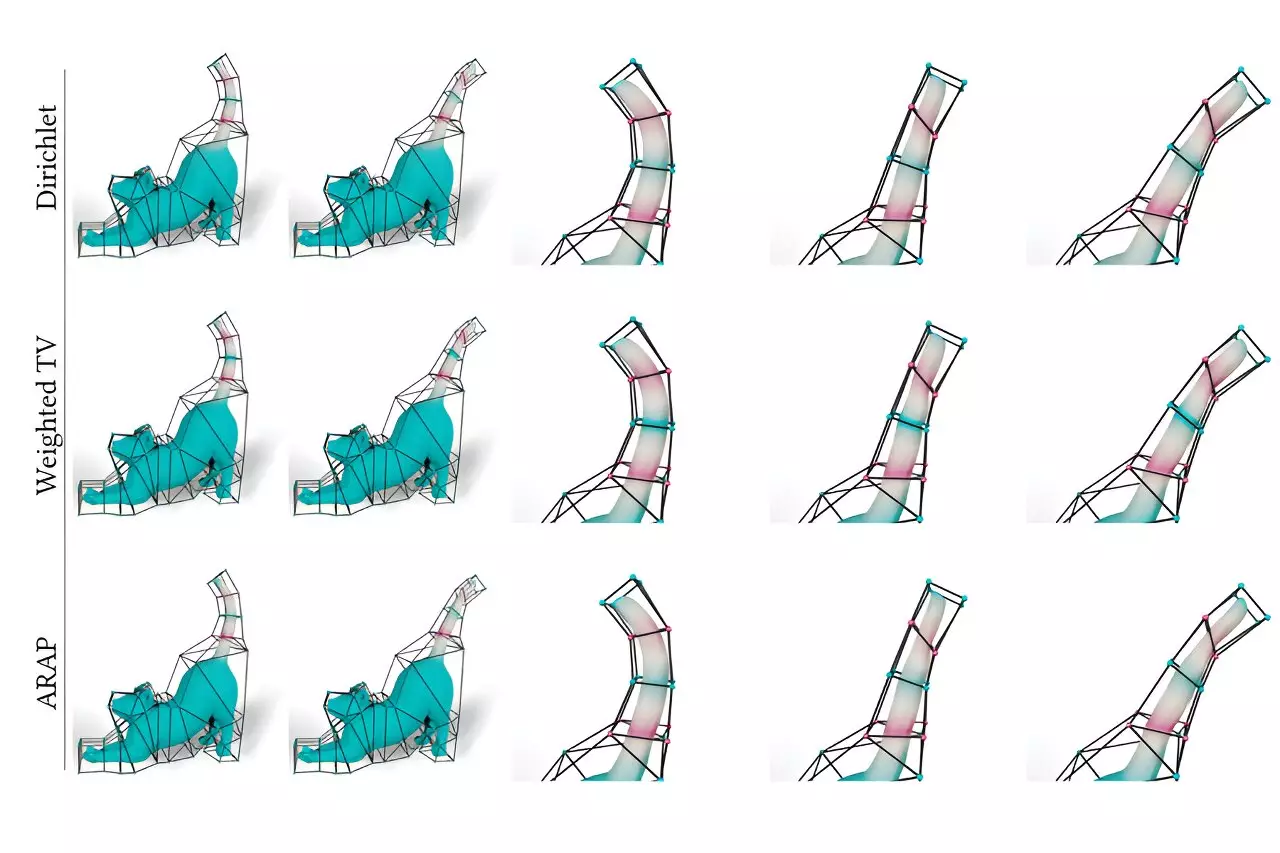
Drawing on the triangular barycentric coordinates introduced by August Möbius in 1827, the researchers devised a method to cover complex shapes with overlapping virtual triangles. These virtual triangles connect triplets of points on the outside of the cage, and each one defines a valid barycentric coordinate function. The challenge then becomes combining these virtual triangles to create a more intricate but smooth function. This is where the neural network steps in, predicting how to merge the barycentric coordinates of the virtual triangles. With this method, artists can experiment with different functions, observe the resulting animation, and tweak the coordinates until they achieve their desired look.
The researchers demonstrated the power of their method through various examples, showcasing how it can generate more natural-looking animations compared to other approaches. One such example involved a cat’s tail that curves smoothly when it moves, as opposed to folding rigidly near the vertices of the cage. The flexibility offered by neural networks allows artists to explore and iterate on their animations in real time, revolutionizing the creative process. With this newfound control, artists can shape their vision with greater precision and bring characters to life in ways previously thought impossible.
Beyond its impact on the animation industry, this technique holds immense potential for other fields as well. Medical imaging can benefit from the ability to define and manipulate shapes with greater accuracy. Architectural design can utilize the flexibility to visualize and refine structures in virtual environments. Virtual reality experiences can become more immersive, as objects and characters move realistically. Computer vision systems, particularly those employed by robots, can enhance their understanding of object movement in the real world. The applications are boundless, and this technique opens up new avenues for innovation and exploration.
The introduction of flexible barycentric coordinates and their integration with neural networks is a significant breakthrough for artists and researchers alike. By allowing artists to define and control how shapes move in their animations, this technique empowers creativity and opens up new possibilities in the ever-evolving world of animation. Furthermore, its potential impact on fields beyond animation demonstrates its versatility and applicability across diverse industries. As this method continues to evolve and mature, we can expect to witness a new era of animation and shape manipulation that pushes the boundaries of artistic expression.

Leave a Reply