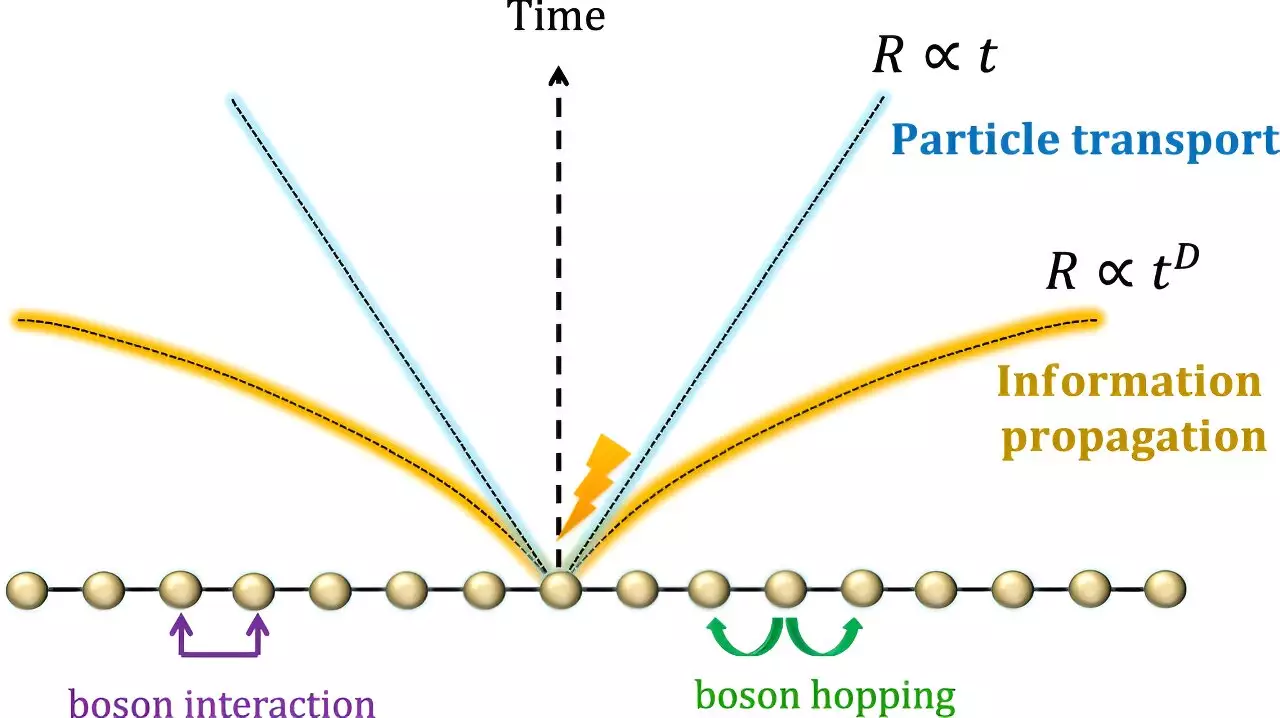
One of the fundamental concepts in quantum many-body systems, such as interacting boson systems like Bose-Einstein condensates (BECs), is the Lieb-Robinson bound. This bound quantifies the speed at which information or changes can propagate through a quantum system. When a change occurs in one part of the system, the Lieb-Robinson bound describes how quickly this change influences other regions within the system. The propagation is limited to an effective light cone, inspired by Einstein’s theory of relativity, which sets a universal speed limit for information transmission in quantum systems.
Interacting boson systems, which consist of multiple bosons like photons, have long presented challenges due to their long-range interactions and unbounded energy. The development of simulations and theoretical models for such systems has been difficult. However, with the introduction of models like the Bose-Hubbard model, insights into the behavior of bosonic systems have been gained. The Bose-Hubbard model considers the hopping and on-site interactions of bosons in a lattice structure, providing a framework to study the dynamics of boson transport.
Results of the Study
The recent study by researchers from Japan focuses on the Lieb-Robinson bound in a D-dimensional lattice governed by the Bose-Hubbard model. Three key results have been identified in the study. Firstly, the speed of boson transport in interacting boson systems is limited, even in the presence of long-range interactions. While the speed grows logarithmically with time, it remains relatively slow, offering insights into the upper bounds of boson dynamics. Secondly, the propagation of operators within the system introduces errors that affect information transmission. These errors determine the speed at which information can propagate, highlighting the importance of minimizing deviations from the ideal evolution of the system. Lastly, interactions among bosons induce clustering in specific regions, facilitating accelerated information propagation along certain paths. This phenomenon, while bounded, exhibits polynomial growth based on the dimensionality of the system.
Comparison with Fermionic Systems
A notable contrast between bosonic and fermionic systems lies in the speed of information propagation. While fermionic systems show a finite speed limit for information transmission, bosonic systems can propagate information faster. The spread of the light cone in bosonic systems is non-linear, accelerating over time as more bosons cooperate. The ability of bosons to occupy the same state simultaneously contributes to the increased speed of information propagation. The findings of this study challenge previous assumptions and provide new insights into the dynamics of interacting boson systems.
The study opens up new possibilities for exploring the behavior of interacting boson systems in terms of information propagation. The algorithm developed by the researchers has the potential to simulate condensed matter physics and aid in the discovery of new quantum phases. Furthermore, it could assist in simulating quantum thermalization processes, shedding light on how closed quantum systems reach a steady state over time. The research by Dr. Tomotaka Kuwahara and his team highlights the significance of understanding quantum systems containing fundamental particles like bosons, paving the way for further investigations into the complexities of quantum information transmission in interacting boson systems.

Leave a Reply